Partie III : La coloration par Welsh-Powel

1. Principe

L’algorithme de Welsh & Powell consiste ainsi à colorer séquentiellement le graphe en visitant les sommets par ordre de degré décroissant. L’idée est que les sommets ayant beaucoup de voisins seront plus difficiles à colorer, et donc il faut les colorer en premier. La complexité de l’algorithme devient O(n ln n + m) en utilisant un tri par comparaison, mais reste O(n + m) avec un tri par dénombrement. Cependant on peut parfois aboutir aux pires colorations possibles ( n 2 au lieu de 2). L’heuristique DSATUR propose une amélioration du principe de l’algorithme de Welsh & Powell afin d’éviter ce problème.

Il y a une certaine procédure à respecter afin de mettre en oeuvre cet algorithme.

Procédure :

1. Repérer le degré de chaque sommet.
2. Ranger les sommets par ordre de degrés décroissants (dans certains cas plusieurs possibilités).
3. Attribuer au premier sommet (A) de la liste une couleur.
4. Suivre la liste en attribuant la même couleur au premier sommet (B) qui ne soit pas adjacent à (A).
5. Suivre (si possible) la liste jusqu’au prochain sommet (C) qui ne soit adjacent ni à A ni à B.
6. Continuer jusqu’à ce que la liste soit finie.
7. Prendre une deuxième couleur pour le premier sommet (D) non encore coloré de la liste.
8. Répéter les opérations 4 à 7.
9. Continuer jusqu’à avoir coloré tous les sommets.

2. Algorithme

1. On note L la liste des sommets si classes suivant l’ordre décroissant de leur
2. degre : d(s1)  d(s2)  d(s3)  :::  d(sn).
4. Initialisation :
5. L : liste des sommets dans l’ordre décroissant du degré
6. couleur = 0
8. Tant que L ≠ ∅ ; faire
9.         couleur=couleur+1
10.         couleur(s) = couleur
11.         Pour tout t dans L faire
12.                 Si t ∉ Γs
13.                         couleur(t)=couleur
14.                         Γs = Γs ∪ Γt
15.                 Fin si
16.         Fin faire
17. Retirer les sommets colores de L
18. Fin faire

 

 

3. Exemples

Prenons ces 5 graphes :

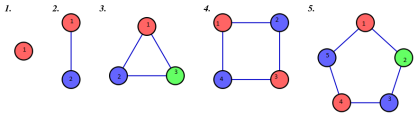
Graphe 1 :

Sommet	Degré	Successeurs
1	0	X

Couleur/Sommet	1
C1 : rouge	C1

 

Graphe 2 :

Sommet	Degré	Successeurs
1	1	2
2	1	1

Couleur/Sommet	1	2
C1 : rouge	C1
C2 : bleu	X	C2

 

Graphe 3 :

Sommet	Degré	Successeurs
1	2	{2,3}
2	2	{1,3}
3	2	{1,2}

Couleur/Sommet	3	2	1
C1 : vert	C1
C2 : bleu	X	C2
C3 : rouge	X	X	C3

 

Graphe 4 :

Sommet	Degré	Successeurs
1	2	{2,4}
2	2	{1,3}
3	2	{2,4}
4	2	{1,3}

Couleur/Sommet	4	3	2	1
C1 : bleu	C1		C1
C2 : rouge	X	C2	X	C2

 

Graphe 5 :

Sommet	Degré	Successeurs
1	2	{2,5}
2	2	{1,3}
3	2	{2,4}
4	2	{3,5}
5	2	{1,4}

Couleur/Sommet	5	4	3	2	1
C1 : bleu	C1		C1
C2 rouge	X	C2	X	C2
C3 : Vert	X	X	X	X	C3

 

4. Contre-exemple

Afin de tester l’efficacité de l’algorithme de Welsh Powell, nous allons mettre en place un contre exemple.

Soit le graphe :

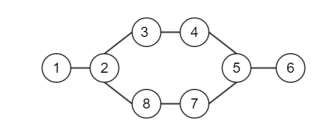
Nous allons dérouler l’algorithme de Welsh Powell normalement :

Sommet	Degré	Successeurs
1	1	2
2	3	{1,3,8}
3	2	{2,4}
4	2	{3,5}
5	3	{4,6,7}
6	1	5
7	2	{5,8}
8	2	{2,7}

 

Couleur/sommet	5	2	8	7	4	3	6	1
C1 (rouge)	C1	C1
C2 (vert)	x	x	C2		C2		C2	C2
C3 (bleu)	x	x	x	C3	x	C3	x	x

 

Avec l’application de l’algorithme, on obtient alors cette coloration :

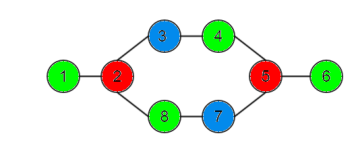
Hors, elle n’est pas optimale.
En effet, seul deux couleurs suffisent pour colorier ce graphe, tel que :

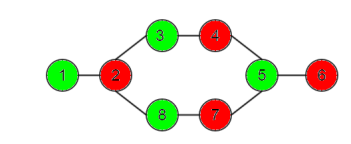
5. Limites

L’algorithme de Welsh Powell permet d’avoir une coloration des sommets cohérente.

Néanmoins, le contre-exemple montre bien que la coloration proposée n’est pas toujours optimale, car dans certains cas, un nombre plus restreint de couleurs peuvent être utilisées (voir ci-dessus).

Il est donc parfois plus simple d’étudier le graphe sans ce dernier et de trouver soi-même une coloration optimale, et ensuite vérifier sa coloration avec l’algorithme pour voir si elle est optimale ou non (à condition que le graphe soit facile de compréhension comme l’est notre contre-exemple).